2023年可积系统及其应用

博士生论坛

 

可积系统及其应用博士生论坛旨在为国内从事非线性可积系统与孤立子理论及其应用研究的在读博士研究生和刚毕业的青年学者（获博士学位的时间不超过两年）搭建学术交流和成果展示的平台，组织优秀博士生进行学习心得交流、科研协同探索，树立榜样、鼓励原创、促进合作。第一届论坛于2023年10月在西安交通大学数学与统计学院举办，参与高校包括郑州大学、陕西师范大学、西北大学和宁波大学。

 

咨询委员会

耿献国（郑州大学）

屈长征（宁波大学）

 

专家委员会

窦井波（陕西师范大学）

付    英（西北大学）

黄    晴（西北大学）

康    静（西北大学）

刘小川（西安交通大学）

王丽真（西北大学）

薛    波（郑州大学）

姚若侠（陕西师范大学）

 

组织委员会

负责人：刘小川（西安交通大学）

成    员：程小雨（西北大学）

姜自文（西北大学）

李晨曦（西安交通大学）

乔    琛（陕西师范大学）

谭懿平（陕西师范大学）

王   嘉（郑州大学）

王云波（西北大学）

严可欣（宁波大学）

种鸽子（西北大学）

（注：组织委员会成员除负责人外均为参与高校博士研究生）

 

会 议 日 程

 

会议时间：2023年10月20日

会议地点：西安交通大学数学楼2-1会议室

 

报告摘要

 

报告人：程小雨（西北大学数学学院）

题  目：Fundamental solutions for conformable time fractional partial differential equations

摘  要：The connections between fundamental solutions and Lie symmetry groups for a class of conformable time fractional partial differential equations (PDEs) with variable coefficient are investigated. The group-invariant solutions to the considered equations are constructed by means of symmetry group method. Then, the corresponding fundamental solutions for these PDEs are established by taking the inverse Laplace transform of the group invariant solutions. In addition, some examples are introduced to illustrate the effectiveness of this approach.

 

报告人：谷琼雅（西北大学数学学院）

题  目：The complete group classification and exact solutions of two types fractional nonlinear partial differential equations

摘  要：The main purpose of this talk is performing the complete group classification and exact solutions of two types of fractional nonlinear partial differential equations. One of these two equations is the space-time fractional generalized porous medium equation with three constant coefficients, the other is the time fractional generalized thin film equation with two variable coefficients. Specifically, power series solutions of the time fractional generalized thin film equation are also derived by means of Erd´elyi-Kober fractional differential operators.

 

报告人：姜自文（西北大学数学学院）

题  目：Mild solution of fractional Keller-Segel-Navier-Stokes system

摘  要：In this talk, we present some results of mild solution for the Cauchy problem of Keller-Segel-Navier-Stokes model with time fractional Caputo differential operator and fractional Laplacian operator, which describes both memory effect and Lévy process of the system. Take advantage of the connections between Mittag-Leffler operators and Mainardi function and the estimates of fractional heat semi-groups, we construct the 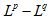   estimates of Mittag-Leffler operators. The local and global existence are established by Banach fixed point theorem and Banach implicit function theorem, respectively. This talk is based on joint works with Prof. Lizhen Wang.

 

报告人：李岩（陕西师范大学计算机科学学院）

题  目：Nonlinear waves and interactional structures under constant wave background for (2+1)-dimensional generalized fifth-order KdV equation

摘  要：The (2+1)-dimensional generalized fifth-order KdV (2GKdV) equation and its breather wave from the N-solitary wave solution with a nonzero background based on the Hirota bilinear method is investigated. Introducing a velocity resonance mechanism for the breather solution, we obtain abundant nonlinear wave structures. Also, distinct nonlinear wave molecules and interactional structures are constructed, of which the dynamical properties are revealed via the phase shifts analysis and the trajectory equations.

 

报告人：刘文豪（郑州大学数学与统计学院）

题  目：Long-time asymptotics for the complex nonlinear transverse oscillation equation

摘  要：In this paper, we study the long-time asymptotic behavior of the Cauchy problem for the complex nonlinear transverse oscillation equation. Based on the corresponding Lax pair, the original Riemann-Hilbert problem is constructed by introducing some spectral function transformations and variable transformations, and the solution of the complex nonlinear transverse oscillation equation is transformed into the solution of the resulted Riemann-Hilbert problem. Various Deift-Zhou contour deformations and the motivation behind them are given, from which the original Riemann-Hilbert problem is further transformed into a solvable model problem. The long-time asymptotic behavior of the Cauchy problem for the complex nonlinear transverse oscillation equation is obtained by using the nonlinear steepest decent method.

 

报告人：马晶晶（陕西师范大学数学与统计学院）

题  目：Hardy-Littlewood-Sobolev inequalities with partial variable weight on the upper half-space and related inequalities

摘  要：In this talk, we establish a class of Hardy-Littlewood-Sobolev inequalities with partial variable weight functions on the upper half-space. We show that the sharp constants in this inequality are attained by the method of concentration compactness principle. The cylindrical symmetry and the classification of extremal functions are discussed by the method of moving planes and method of moving spheres. As applications, we show some weighted Sobolev inequalities with partial variable weight function for Laplacian and fractional Laplacian. This is the joint work with Jingbo Dou.

 

报告人：谭懿平（陕西师范大学计算机科学学院）

题  目：Threshold dynamics for epidemic models with stochastic perturbation

摘  要：The basic reproduction number is generally regarded as the important threshold parameter to determine whether the disease goes extinct or not. In this talk, we investigate the impact of environmental perturbations on the epidemic dynamics around our proposed stochastic epidemic models. Through defining stochastic basic reproduction numbers, the sufficient conditions for the stochastic extinction and persistence of the disease are given. Moreover, an important task we do is to reduce the gap between the threshold conditions, thus making efforts to show the dynamics as fully as possible. The theoretical results and the related numerical experiments dual confirm the crucial role of random environmental noises in the process of disease. The main results can be concluded as: (i) strong stochastic perturbations seem to make the disease die out with probability one; (ii) the distributions of the solutions for the stochastic models becomes more dispersed as the noise intensities increase. These may provide us certain useful control strategies to regulate infectious disease dynamics.

 

报告人：王嘉（郑州大学数学与统计学院）

题  目：Riemann-Hilbert approach and N-soliton solutions for a negative matrix AKNS system with a Hermitian symmetric space

摘  要：In this paper, the Riemann-Hilbert approach is used to solve a negative matrix AKNS system with a Hermitian symmetric space. Through spectral analysis, a Riemann-Hilbert problem is established on the real axis, then N-soliton solutions of the negative matrix AKNS system are obtained by solving the non-regular Riemann-Hilbert problem under the reflectionless condition. Furthermore, some figures of these explicit solutions are plotted, which are proved to be of solitary features.

 

报告人：吴孝平（西北大学数学学院）

题  目：Reducibility of a class of operators arising from the dispersive third-order Benjamin-Ono equation

摘  要： We prove the reducibility of a class of quasi-periodically time-dependent linear operators, which are derived from linearizing the dispersive third-order Benjamin-Ono equation on the circle at a small amplitude quasi-periodic function, with a diophantine frequency vector 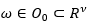 . It is shown that there exists a set  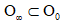 of asymptotically full Lebesgue measure such that for any  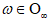, the operators can be reduced to the ones with constant coefficients by some linear transformations depending on time quasi-periodicity. These transformations include a change of variable induced by a diffeomorphism of the torus, the flow of some PDEs and a pseudo-differential operator of order zero, which are real, reversibility-preserving and satisfy the sharp tame bounds. We first reduce the linearized operator of order three to the one with constant coefficients plus a remainder of order zero, and then a perturbative reducibility scheme is performed. This work will be the first fundamental step in proving the existence of time quasi-periodic solutions for the dispersive third-order Benjamin-Ono equation.

 

报告人：徐静（西安交通大学数学与统计学院）

题  目：The critical-equation method for optimal recovery of weights in Sturm-Liouville eigenvalue theory

摘  要：In this talk, we study the extremal problem of the L1-norm of weights in the case of two given eigenvalues. By establishing the critical equation, the expression of the weight function at the extreme point is obtained, and we obtain the relationship between the first two eigenvalue ratios and the extremal problem of the L1-norm of weights.

 

报告人：严可欣（宁波大学数学与统计学院）

题  目：Peakon solutions of the $\mu$-$fg$ family and ill-posedness of the $\mu$-Camassa-Holm type equations

摘  要：This talk introduces a family of general nonlinear dispersive wave equations containing ordinary periodic integrable equations with single peakon and multi-peakon solutions. The main result is that we use the distribution theory to show the sufficient and necessary conditions for the existence of single peakon and multi-peakon solutions of this family of equations. Secondly, constructing a 2-peakon solution with an (a)symmetric peakon-antipeakon initial profile, analyzing the dynamical behavior of the 2-peakon solution, we study ill-posedness of the Cauchy problem for the $\mu$-$b$ family and modified $\mu$-Camassa-Holm equation in the Sobolev spaces.

 

报告人：尹子涵（西北大学数学学院）

题  目：Dispersive revival and fractalization for multi-component dispersive equations

摘  要：The research of dispersive revival and fractalization in scalar dispersive equations is complete. In this talk, we focus on the periodic initial boundary problem of multi-component dispersive equations. Firstly, we get the dispersive quantization condition of the two-component dispersive equations. Secondly, we get the new revival phenomena for the bidirectional hyperbolic dispersive equations. Finally, we focus on the Manakov system which is a classical Schrodinger type system. We get the regularity of the Manakov system on the torus and the fractal dimensional of the fractal solution of the Manakov system.

 

报告人：种鸽子（西北大学数学学院）

题  目：Orbital stability of periodic peakons for a new higher-order μ-Camassa–Holm equation

摘  要：The consideration here is a higher-order μ-Camassa–Holm equation, which is a higher-order extension of the μ-Camassa–Holm equation and retains some properties of the μ-Camassa–Holm equation and the modified μ-Camassa–Holm equation. By utilizing the inequalities with the maximum and minimum of solutions related to the first three conservation laws, we establish that the periodic peakons of this equation are orbitally stable under small perturbations in the energy space.

 

报告人：朱晨迪（西北大学数学学院）

题  目：A four-component Camassa-Holm-type system

摘  要：We propose a four-component Camassa-Holm-type system which contains an arbitrary function G. The Lax pair and infinite conservation laws of this system are constructed. We derive the Hamiltonian structures and N-peakon solutions of the four-component system for the special choices of G. In particular, the “M/W”-shape-peaked solitons are obtained.