西安几何拓扑会议

 

 

 

 

 

 

2019.9.20-22

西安交通大学 数学与统计学院

 

 

l  会议时间、地点

2019.9.20-22，西安交通大学 数学楼 2-1会议室

 

l  入住酒店

馨乐庭兴庆宫服务公寓

地址：西安市碑林区兴庆路159号，Tel: (029)83380587

交大康桥宾馆

地址：西安市碑林区交大商业街，Tel：(029)82666366

 

l  用餐地点

交大康桥酒楼（康桥宾馆二楼）

 

l  会议签到

9月19日12:00-22:00，馨乐庭大堂，签到并领取会议材料

 

l  组织者

赵彬 Email：zhaobinmathATxjtu.edu.cn

张强 Email：zhangq.mathATxjtu.edu.cn

 

l  资助方

国家天元数学西北中心

国家自然科学基金NSFC#11771345

会议日程

 

 

报告题目、摘要

 

陈海苗（北京工商大学）

题目：Representation varieties and character varieties of links

 

陈亮（东北师范大学）

题目：Legendrian duality and its applications

摘要：We first introduce a basic Legendrian duality among pseudo spheres in semi-Euclidean space. As its applications, I will investigate caustics of the fronts in 2-dimensional hyperbolic space and singularities of Gauss maps of the degenerate surfaces in 4-dimensional Anti de Sitter space.

 

杜晓明（华南理工大学）

标题：不可定向曲面映射类群以及 Dehn twist 子群的有限阶生成元集

Title: The torsion generating set of the mapping class groups and Dehn twist subgroups of non-orientable surfaces

摘要：设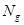是亏格为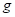的不可定向曲面，我们证明当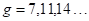时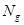，的映射类群可被3个有限阶元素生成；当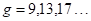时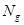，的映射类群中的 Dehn twist 子群可被3个有限阶元素生成。

 

段海豹（中国科学院）

题目：On the multi-degree of coverings on Lie groups

摘要：For a Lie group G with center Z(G) consider the covering map c:G→PG:=G/Z(G). The induced map c^{∗}:H^{∗}(PG)→H^{∗}(G) on the integral cohomologies gives rise to a sequence D(G;PG) of integers, called the multi-degree of the covering c. We determine the sequence D(G;PG) for all 1-connected simple Lie groups with non-trivial centers.

 

李平（同济大学）

题目： The rigidity on the second fundamental form of projective manifolds

摘要：We review some known gap phenomena related to the second fundamental form of the minimal submanfolds and complex submanifolds in the unit spheres and complex projective spaces respectively, and then present our recent progress on them.

 

李友林（上海交通大学）

题目: Smoothly non-isotopic Lagrangian disk fillings of Legendrian knots

摘要: In this talk, we construct families of distinct Lagrangian ribbon disks in the standard symplectic 4-ball which have the same boundary Legendrian knots, and are not smoothly isotopic or have non-homeomorphic exteriors.  This is joint work with Motoo Tange.

 

吕志（复旦大学）

题目：On orbit braids

摘要：Let M be a connected topological manifold of dimension at least 2 with an effective action of a finite group G. Associating with the orbit configuration space F_G(M, n), n ≥ 2 of the G-manifold M, we try to upbuild the theoretical framework of orbit braids in M × I where the action of G on I is trivial, which contains the following contents: we introduce the orbit braid group B_n^{orb}(M, G), and show that it is isomorphic to a group with an additional endowed operation (called the extended fundamental group), formed by the homotopy classes of some paths (not necessarily closed paths) in F_G(M, n), which is an essential extension for fundamental groups. The orbit braid group B_n^{orb}(M, G) is large enough to contain the fundamental group of F_G(M, n) and other various braid groups as its subgroups. Around the central position of B_n^{orb}(M, G), we obtain five short exact sequences weaved in a commutative diagram. We also analyze the essential relations among various braid groups associated to those configuration spaces F_G(M, n), F(M, n), and F(M/G, n). We finally consider how to give the presentations of orbit braid groups in terms of orbit braids as generators. We carry out our work by choosing M = ℂ ≈ ℝ2 with typical actions of ℤp and (ℤ2)2. We obtain the presentations of the corresponding orbit braid groups, from which we see that the generalized braid group Br(Dn) (introduced by Brieskorn) actually agrees with the orbit braid group B_n^{orb}(ℂ\{0}, ℤ2) and Br(Dn) is a subgroup of the orbit braid group B_n^{orb}(ℂ, ℤ2). This talk is based upon a joint work with Hao Li and Fengling Li.

 

马继明(复旦大学)

题目: Compact 4-dimensional hyperbolic Coxeter polytopes with eight facets

摘要:  We give the classification of all the compact 4-dimensional hyperbolic Coxeter polytopes with eight facets, the proof uses geometrical, combinatorial, and computational techniques. This is a joint work with Fangting Zheng.

 

 

 

邱瑞锋（华东师范大学）

题目：Heegaard splitting, a survey.

摘要：TBA

 

王宏玉（扬州大学）

题目：On signed Euler Characteristic

摘要：In this talk, we discuss the Chern-Hopf conjecture. Let M be a closed symplectic manifold of dimension 2n with non-ellipticity. We can de ne an almost Kahler structure on M by using the given symplectic form. Using Darboux coordinate charts, we deform the given almost Kahler structure to obtain a homotopy equivalent Lipschitz Kahler structure on the universal covering of M. Analogous to Teleman's L2-Hodge decomposition on PL manifolds or Lipschitz Riemannian manifolds, we give a L2-Hodge decomposition theorem on the universal covering of M w.r.t. the measurable Kahler metric. Using an argument of Gromov, we give a vanishing theorem for L2 harmonic p-forms, p 6= n (resp. a non-vanishing theorem for L2 harmonic n-forms) on the universal covering of M which is d(sublinear) (resp. d(bounded)), then its signed Euler characteristic satisfies (􀀀1)n­(M)  0 (resp. (􀀀1)n­(M) > 0). As an application, we show that the Chern-Hopf conjecture holds true in closed even dimensional Riemannian manifolds with nonpositive curvature (resp. strictly negative curvature), it gives a positive answer to a Yau's problem due to S. S. Chern and H. Hopf.

 

王家军（北京大学）

TBA

 

王诗宬（北京大学）

题目：Some remarks on extending  periodical maps on surfaces

 

吴建春（苏州大学）

题目: GL_d(\Z)中的一些算法问题
摘要: 介绍一些几何群论尤其是关于一般线性群GL_d(\Z)的算法问题.

 

杨文元（北京大学）

题目：Martin boundary of random walks on groups 

摘要：我们将介绍群上的随机游走的基本概念和理论，侧重于带非正曲率的群的Possion边界和Martin边界的确定问题。我们将介绍双曲群，相对双曲群的已知的结果，以及正在进行的带收缩元素的群的一些相关工作介绍。

 

叶圣奎（西交利物浦大学）

题目:  Rigidity of matrix group actions on CAT(0) spaces with possible parabolic isometries 

摘要: It is well-known that SLn(Qp) acts without fixed points on an (n-1)- dimensional CAT(0) space (the affine building). We prove that n-1 is the smallest dimension of CAT(0) spaces on which matrix groups act without fixed points. Explicitly, let R be an associative ring with identity and E_n(R) the extended elementary subgroup. Any isometric action of E_n(R) on a complete CAT(0) space X^d of dimension d < n-1 has a fixed point. Similar results are discussed for automorphism groups of free groups.

 

张影（苏州大学）

题目： Comparison of minimal equal lengths in a once punctured torus running over its relative Teichmuller space

摘要： We consider the problem of minimizing the equal length of a pair of simple closed geodesics of given topological type in a once punctured hyperbolic torus with fixed geometric boundary data as the torus runs over its relative Teichmuller space. For specific pairs with symmetry, we are able to determine the minimizing torus and hence the minimal length. It is natural to compare the minimal lengths for inequivalent pair of the same intersection number. As computer experiments show, there is a conjecture that the specific pair of slopes (1/0, 1/n) has its minimal length smaller than any other pair of slopes (1/0, m/n), regardless of the geometric boundary data. In joint work with Da Lei, we obtain a stronger result as the geometric boundary of the torus is a conic point and the cone angle is approaching $2\pi$.

 

赵学志（首都师范大学）

题目：Geometric intersections numbers of loops on surfaces

摘要：Given two loops on a compact surfaces $F$, it is natural to ask: what is their minimal intersection number during homotopy classes?  This number is usually said to be the geometric intersection number. In this talk, we shall explain a way to determine the geometric intersection and self-intersection numbers of loops on surfaces.  Our integration are Nielsen fixed point theory and Gr\"{o}bner-Shirsov basis. We illustrate an application: An algorithm to compute the distance of loops in curve complex. This talk includes a joint work with Gu Ying.

 

邹燕清（大连民族大学）

题目：Mapping class group of a Heegaard splitting

摘要：We will introduce some recent results on mapping class group of a Heegaard splitting.

 

与会者

序号	姓名	工作单位	序号	姓名	工作单位
1	毕婉莹	哈尔滨师范大学	35	王春晓	哈尔滨师范大学
2	蔡力	西交利物浦大学	36	王海伟	西安交通大学
3	曹涛涛	西安交通大学	37	王宏玉	扬州大学
4	陈海苗	北京工商大学	38	王家军	北京大学
5	陈亮	东北师范大学	39	王诗宬	北京大学
6	陈小杨	同济大学	40	王彦英	河北师范大学
7	陈新红	西南交通大学	41	王咏乔	大连海事大学
8	陈智	合肥工业大学	42	翁文	华南师范大学
9	丁雁鸿	河北师范大学	43	邬恩信	汕头大学
10	杜晓明	华南理工大学	44	吴建春	苏州大学
11	段海豹	中科院数学所	45	夏常春	西安交通大学
12	鄂强	大连海事大学	46	谢治琦	榆林学院
13	方复全	首都师范大学	47	徐杰	陕西师范大学
14	高红铸	北京师范大学	48	延卫军	榆林学院
15	何正茂	陕西师范大学	49	杨会军	河南大学
16	姜伯驹	北京大学	50	杨建强	红河学院
17	雷达	苏州大学	51	杨文元	北京大学
18	雷逢春	大连理工大学	52	杨云龙	大连海事大学
19	李风玲	大连理工大学	53	杨志青	大连理工大学
20	李平	同济大学	54	叶圣奎	西交利物浦大学
21	李体耀	重庆师范大学	55	于浩然	吉林大学
22	李彦霖	杭州师范大学	56	张丛磊	河北师范大学
23	李友林	上海交通大学	57	张东	天津城建大学
24	梁良	辽宁师范大学	58	张发泽	东北师范大学
25	刘思瑶	哈尔滨师范大学	59	张强	西安交通大学
26	刘西民	大连理工大学	60	张晓玲	新疆大学
27	刘晔	西交利物浦大学	61	张影	苏州大学
28	鲁静	西安交通大学	62	张志国	河北师范大学
29	吕志	复旦大学	63	赵彬	西安交通大学
30	马继明	复旦大学	64	赵浩	华南师范大学
31	邱瑞锋	华东师范大学	65	赵旭安	北京师范大学
32	阮祥龙	西安交通大学	66	赵学志	首都师范大学
33	沈广艳	东北师范大学	67	邹燕清	大连民族大学
34	苏阳	中科院数学院

 

交通信息

1.      西安咸阳国际机场——馨乐庭兴庆宫公寓

l      出租车：约70分钟，150元

l      机场巴士https://mp.weixin.qq.com/s/xzh6AqBdmoe4YUG1IrbW0g

注：各线路车票（25元）通用，建议乘坐钟楼线、西安火车站线或东二环建国饭店线到终点（哪条线先发车乘哪条），然后出租车至馨乐庭（<15分钟，<15元）

 

2.      西安北站——馨乐庭兴庆宫公寓

l       最快捷： 西安北站出检票口乘地铁2号线(末班车23:50)到永宁门（11站、30分钟）出D2口，换乘出租车至馨乐庭（约10分钟，10元）或换乘公交800或402到咸宁路兴庆路口（15分钟）下车步行200米至馨乐庭。

l       西安北站出检票口乘地铁2号线至小寨换乘3号线至咸宁路出B2口，步行1000m至馨乐庭

l       出租车：约50分钟，70元

 

3.      西安站——馨乐庭兴庆宫公寓

l          出租车：约20分钟，20元

l          出火车站直行100米至公交车站，乘607或者602路至咸宁路兴庆路口（约20分钟）下车步行200米至馨乐庭

 

4.       住康桥宾馆的老师和同学，请先到馨乐庭兴庆宫公寓报到，然后由我们带您去康桥宾馆入住。

 

5.      西安南站、阿房宫站很远且交通不便，不建议在此站下车。西安地铁公交支持微信及支付宝等扫码乘车，使用方法如下：

 

微信——>发现——>小程序——>乘车码——>城市选择西安——>地铁或者公交长安通乘车码

 

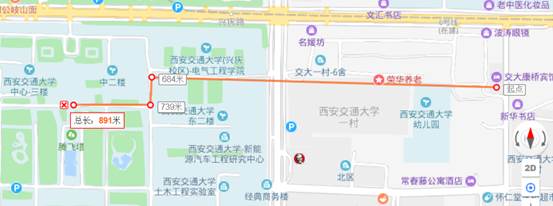
馨乐庭至数学楼（理科楼）700m，路线图

 

 

 

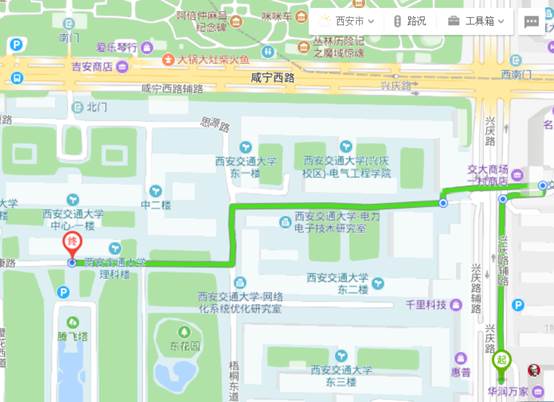
康桥宾馆（酒楼）至数学楼900m，路线图

 

国家天元数学西北中心（以下简称“中心”）是国家自然科学基金委员会天元数学基金为推动中国数学率先赶上世界先进水平、推动中国数学区域、领域均衡发展而设立的数学研究机构（平台）。

中心的定位是：依托交大、立足西北、面向全国、放眼世界，建设数学工作者与其它学科领域学者深度交叉融合的学术交流中心和数学与数学技术研究中心。目标是：逐步将中心建设成为中国数学与其他学科交叉前沿研究基地、国家重大任务承接地、数学与数学技术研发基地与人才集聚地，新一代应用数学创新人才培养基地。

中心的主要任务包括：面向学科前沿开展学术交流，面向国家重大需求组织重大交叉问题研讨和重大课题研究；实施“天元学者/博士后”项目，促进数学研究与人才培养的地区平衡；策划并举办“全国应用数学暑期学校”及“全国大学数学教师暑期学校”，促进我国的应用数学发展及中西部地区大学数学教师队伍的培养。

中心依托西安交通大学，协同西北工业大学、兰州大学、西安电子科技大学、西北大学、陕西师范大学、新疆大学、西北师范大学、宁夏大学、青海师范大学等九所西部高校联合建设。中心支持各联建单位开展具有地域特色、符合各校情况的学术活动。

 

国家天元数学西北中心组织架构图